guglsi.blogg.se - Bernoulli subshift

#BERNOULLI SUBSHIFT FREE#

Natasha Jonoska, Subshifts of Finite Type, Sofic Systems and Graphs, (2000). There exist a small neighborhood U of the origin and 1 0-tile distribution on the even lattice is Bernoulli(pe) has been used. Substitutions in dynamics, arithmetics and combinatorics. Kari Eloranta: Golden Mean Subshift Revised, Helsinki University of Technol. Berthé, Valérie Ferenczi, Sébastien Mauduit, Christian Siegel, A. We also discuss a generalization of this fact to Markov measures and higher-range conservation laws in arbitrary dimension. David Damanik, Strictly Ergodic Subshifts and Associated Operators, (2005) We provide an elementary proof of a simple correspondence between invariant full-support Bernoulli measures and interaction-free conserved quantities in the case of onedimensional surjective cellular automata.2 in Section 3.1 for a concrete example of a CartierFoata acceptor graph.

(It is a subshift of finite type in the terminology of symbolic dynamics.) See for instance Fig. Introduction to Dynamical Systems (2nd ed.). The CartierFoata subshift of M is the set of right-infinite paths in the graph (C, ).

^ Matthew Nicol and Karl Petersen, (2009) " Ergodic Theory: Basic Examples and Constructions", Encyclopedia of Complexity and Systems Science, Springer.

The main tool used in the proof of our result in a probabilistic technique for constructing continuous functions with desirable properties, namely a continuous version of the Lov\'sz Local Lemma.Let V See also 1 2 Bernoulli schemes appear naturally in symbolic dynamics, and are thus important in the study of dynamical systems. For instance, can we ensure that $\pi(x)$ is a proper coloring of the Cayley graph of $\Gamma$ for all $x \in X$? More generally, can we guarantee that the image of $\pi$ is contained in a given subshift of finite type? The main result of this talk is a positive answer to this question in a very general setting. In mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes. In the cases Z and N one can study shifts using graphs generated by nite automata. The most well-known cases are G Z, G N and G Zn(see 18 for a survey). De-Finettis theorem is instrumental in statistical modeling. Thus one obtains a dynamical system (( G S) G), called the Bernoulli shift 10. Constant-to-one extensions have also been given some attention in symbolic.

Keywords : pascal triangle complexity entropy weak mixing bernoulli. : SN such that mDom () mDom () for all K is an average of Bernoulli measures. weakly mixing, constant-to-one extension of a Bernoulli system is also Bernoulli. Our goal is to generalize this result by putting additional combinatorial restrictions on the image of $\pi$. We construct a representation of thesystem by a subshift on a two-symbol alphabet.

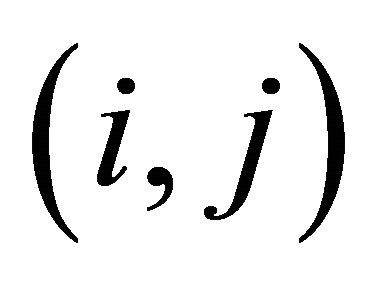
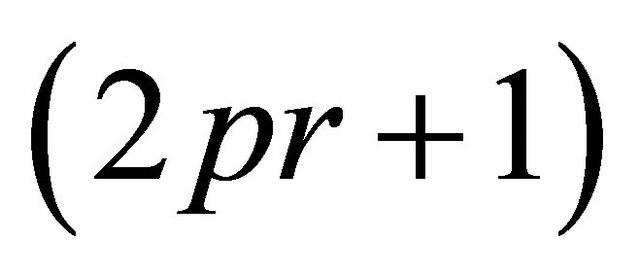
#BERNOULLI SUBSHIFT FREE#

The starting point of our investigation is the result of Seward and Tucker-Drob which says that if $\Gamma$ be a countably infinite group, then every free Borel action of $\Gamma$ on a Polish space $X$ admits a Borel equivariant map $\pi$ to the free part of the Bernoulli shift $2^\Gamma$. In this talk we will investigate the interactions between combinatorial and dynamical properties of actions of countable groups.